Rabu, 02 Oktober 2013
PENDIDIKAN: Pengertian Silabus dan RPP
PENDIDIKAN: Pengertian Silabus dan RPP: SILABUS DAN RPP(RENCANA PELAKSANAAN PEMBELAJARAN) TEMATIK SILABUS 1.Pengertian Silabus Silabus adalah rencana pembelajaran pada suatu kelom...
Kamis, 30 Mei 2013
Rabu, 29 Mei 2013
Firman Tuhan yang diberikan kepada Susan Davis tanggal 18 dan 19 Mei 2013 - Surat Tuhan - Pengangkatan (Rapture), Antikris & Kesaksian
Firman Tuhan yang diberikan kepada Susan Davis tanggal 18 dan 19 Mei 2013 - Surat Tuhan - Pengangkatan (Rapture), Antikris & Kesaksianhttp://surattuhan.malang3000.com/?-firman-tuhan-yang-diberikan-kepada-susan-davis-tanggal-18-dan-19-mei-2013-814%2C815
Senin, 27 Mei 2013
KUMPULAN SOAL UJIAN MASUK STAN PILIHAN: PAKET SOAL SOAL PILIHAN UJIAN MASUK STAN
KUMPULAN SOAL UJIAN MASUK STAN PILIHAN: PAKET SOAL SOAL PILIHAN UJIAN MASUK STAN: USM STAN TAHUN 201 3 sudah di depan mata, apakah kita sudah siap untuk menghadapi USM STAN TAHUN 2013 besuk? Dalam menghadapi USM STAN ...
Jumat, 17 Mei 2013
awal blog: Hutan rimba Borneo merupakan ilusi: pepohonan tum...
awal blog:
Hutan rimba Borneo merupakan ilusi: pepohonan tum...awal blog: Hutan rimba Borneo merupakan ilusi: pepohonan tum...: Hutan rimba Borneo merupakan ilusi: pepohonan tumbuh di padang pasir Dilucuti dari tetumbuhan, Borneo menjadi sebuah lahan pembu...
Hutan rimba Borneo merupakan ilusi: pepohonan tum...awal blog: Hutan rimba Borneo merupakan ilusi: pepohonan tum...: Hutan rimba Borneo merupakan ilusi: pepohonan tumbuh di padang pasir Dilucuti dari tetumbuhan, Borneo menjadi sebuah lahan pembu...
Rabu, 15 Mei 2013
10 tips untuk selalu senyum :)
10 Tips Manfaat Tersenyum :

1. Senyum membuat kita lebih menarik
Kita akan selalu tertarik pada orang yang selalu tersenyum. Orang yang selalu tersenyum punya daya tarik tersendiri. Wajah yang berkerut, cemberut, membuat orang menjauh dari kita , tetapi sebaliknya senyum bisa membuat mereka tertarik.
2. Senyum mengubah mood kita
Ketika kita merasa jatuh atau “down” cobalah untuk tersenyum. Mungkin saja mood kita akan berubah menjadi lebih baik.
3. Senyum dapat merangsang orang lain tersenyum
Ketika seseorang tersenyum maka senyum tersebut akan membuat suasana menjadi lebih cerah, mengubah mood orang lain yang ada disekitarnya dan membuat semua orang menjadi senang. Orang yang suka tersenyum membawa kebahagiaan buat orang yang ada di sekitarnya. Seringlah tersenyum maka Kamu akan disukai oleh banyak orang.
4. Senyum dapat mengurangi stres
Jika tanda-tanda stres menyerang kamu, maka wajah Kamu sangat tidak enak untuk dipandang, sesegera mungkin untuk tersenyum karena senyum membantu mencegah kesan bahwa kita sebenarnya sedang stres, lelah atau merasa “down”. Jika Kamu sedang stres cobalah untuk tersenyum, maka stres Kamu akan berkurang dan Kamu akan merasa lebih baik untuk membuat langkah selanjutnya.
5. Senyum meningkatkan sistem imun (kekebalan) tubuh
Senyum dapat membantu kerja imun tubuh agar dapat bekerja dengan baik. Ketika Kamu tersenyum, fungsi imun meningkatkan kemungkinan Kamu menjadi lebih rileks.
6. Senyum menurunkan tekanan darah
Ketika Kamu tersenyum, maka tekanan darahmu akan menurun. Jika Kamu gak percaya, Kamu boleh mencobanya sendiri, jika Kamu memiliki alat pengukur tekanan darah di rumah.
7. Senyum mengeluarkan endorphins (pereda rasa sakit secara alami) dan serotonin
Beberapa studi telah menunjukkan bahwa senyum dapat merangsang pengeluaran endorphin, pereda rasa sakit yang alami, serta serotonin. Senyum memang obat yang alami.
8. Senyum dapat melenturkan kulit wajah dan membuat Kamu terlihat lebih muda
Otot-otot yang digunakan untuk tersenyum ikut membuat Kamu terlihat lebih muda. Jika Kamu ingin sesuatu yang beda, maka berikan senyummu sepanjang hari, maka Kamu akan terlihat lebih muda dan merasa lebih baik. Karena itu dapat Menghilangkan Jerawat juga.
9. Senyum membuat Kamu tampak sukses
Orang yang tersenyum terlihat lebih percaya diri dalam menjalani hidupnya. Cobalah tersenyum saat Kamu melakukan pertemuan dan saat ada janji. Rekan-rekan kerja, sahabat, orang-orang terdekat Kamu akan merasakan sesuatu yang berbeda dan sukses.
10. Senyum membuat Kamu tetap positif
Senyumlah! Lalu sekarang cobalah berpikir sesuatu yang negatif tanpa berhenti tersenyum. Sulitkan? Karena ketika Kamu tersenyum maka senyum tersebut akan mengirimkan sinyal ke tubuh Kamu bahwa “hidup Kamu saat ini baik-baik saja”.
Maka jauhkan diri Kamu dari depresi, stres dan rasa khawatir dengan satu kata yaitu "senyum", tentu saja dengan memberikan senyum pada tempat dan suasana yang tepat. Jika berlebihan, maka orang lain akan menganggap Kamu kurang waras.

1. Senyum membuat kita lebih menarik
Kita akan selalu tertarik pada orang yang selalu tersenyum. Orang yang selalu tersenyum punya daya tarik tersendiri. Wajah yang berkerut, cemberut, membuat orang menjauh dari kita , tetapi sebaliknya senyum bisa membuat mereka tertarik.
2. Senyum mengubah mood kita
Ketika kita merasa jatuh atau “down” cobalah untuk tersenyum. Mungkin saja mood kita akan berubah menjadi lebih baik.
3. Senyum dapat merangsang orang lain tersenyum
Ketika seseorang tersenyum maka senyum tersebut akan membuat suasana menjadi lebih cerah, mengubah mood orang lain yang ada disekitarnya dan membuat semua orang menjadi senang. Orang yang suka tersenyum membawa kebahagiaan buat orang yang ada di sekitarnya. Seringlah tersenyum maka Kamu akan disukai oleh banyak orang.
4. Senyum dapat mengurangi stres
Jika tanda-tanda stres menyerang kamu, maka wajah Kamu sangat tidak enak untuk dipandang, sesegera mungkin untuk tersenyum karena senyum membantu mencegah kesan bahwa kita sebenarnya sedang stres, lelah atau merasa “down”. Jika Kamu sedang stres cobalah untuk tersenyum, maka stres Kamu akan berkurang dan Kamu akan merasa lebih baik untuk membuat langkah selanjutnya.
5. Senyum meningkatkan sistem imun (kekebalan) tubuh
Senyum dapat membantu kerja imun tubuh agar dapat bekerja dengan baik. Ketika Kamu tersenyum, fungsi imun meningkatkan kemungkinan Kamu menjadi lebih rileks.
6. Senyum menurunkan tekanan darah
Ketika Kamu tersenyum, maka tekanan darahmu akan menurun. Jika Kamu gak percaya, Kamu boleh mencobanya sendiri, jika Kamu memiliki alat pengukur tekanan darah di rumah.
7. Senyum mengeluarkan endorphins (pereda rasa sakit secara alami) dan serotonin
Beberapa studi telah menunjukkan bahwa senyum dapat merangsang pengeluaran endorphin, pereda rasa sakit yang alami, serta serotonin. Senyum memang obat yang alami.
8. Senyum dapat melenturkan kulit wajah dan membuat Kamu terlihat lebih muda
Otot-otot yang digunakan untuk tersenyum ikut membuat Kamu terlihat lebih muda. Jika Kamu ingin sesuatu yang beda, maka berikan senyummu sepanjang hari, maka Kamu akan terlihat lebih muda dan merasa lebih baik. Karena itu dapat Menghilangkan Jerawat juga.
9. Senyum membuat Kamu tampak sukses
Orang yang tersenyum terlihat lebih percaya diri dalam menjalani hidupnya. Cobalah tersenyum saat Kamu melakukan pertemuan dan saat ada janji. Rekan-rekan kerja, sahabat, orang-orang terdekat Kamu akan merasakan sesuatu yang berbeda dan sukses.
10. Senyum membuat Kamu tetap positif
Senyumlah! Lalu sekarang cobalah berpikir sesuatu yang negatif tanpa berhenti tersenyum. Sulitkan? Karena ketika Kamu tersenyum maka senyum tersebut akan mengirimkan sinyal ke tubuh Kamu bahwa “hidup Kamu saat ini baik-baik saja”.

Maka jauhkan diri Kamu dari depresi, stres dan rasa khawatir dengan satu kata yaitu "senyum", tentu saja dengan memberikan senyum pada tempat dan suasana yang tepat. Jika berlebihan, maka orang lain akan menganggap Kamu kurang waras.
Jumat, 10 Mei 2013
Rabu, 08 Mei 2013
BELAJAR CEPAT LIMIT FUNGSI
Berapa teorema limit:
Bila
Lim f(x) = A dan Lim g(x) = B
x → a x →a
Maka
1.
Lim [k.f(x)] = k Lim f(x)
x→a x→a
= k. A
2.
Lim [f(x)+g(x)] = Lim f(x) + Lim g(x)
x→a x→a x→a
= A + B
3.
Lim [f(x) x g(x)]
x→a
= Lim f(x) x Lim g(x)
x→a x→a
= A x B
4. Lim f(x) Lim f(x)
x→a g(x)
= x→a . = A
Lim g(x) B
Kamis, 02 Mei 2013
SOLUSI CEPAT MENYELESAIKAN SOAL MATEMATIKA DENGAN RUMUS SMART..
Rumus Smart MateMatika....
Hai… Selamat datang para pencari RUMUS CEPAT MATEMATIKA , Berikut
ini kami sediakan beberapa rumus cepat matematika yang di ambil dari
berbagai sumber… jadi bagi para master, ijin pake rumusnya ya he… .
Rumus Cepat Matematika ini hanya sekedar referensi saja, karena
meskipun namanya rumus cepat tapi kan tetep saja pada prakteknya Anda
harus berbekal dasarnya, rumus-rumus ini gak akan ada manfaatnya sama
sekali kalau belum tau sama sekali dasar-dasar materinya. Ibarat punya
kue dan mau di potong-potong trus ada alat pemotongnya ;
gergaji;pisau;kampak;parang; dan “Bedog”. Alat Potong Mana yang mau Anda
pakai?????
PENTING!!!
Rumus-Rumus yang di sampaikan di sini hanya berlaku pada jenis-jenis soal tertentu saja, dalam arttian, GAK SEMUA SOAL BISA PAKE RUMUS CEPAT !!!!
Here we go….
Berikut adalah salah satu Rumus Cepat, Cekidot…
 Bandingkan solusi biasa dengan Cara SMART-nya. Cepet bangeeeets…..
Bandingkan solusi biasa dengan Cara SMART-nya. Cepet bangeeeets…..

GodBless us...
PENTING!!!
Rumus-Rumus yang di sampaikan di sini hanya berlaku pada jenis-jenis soal tertentu saja, dalam arttian, GAK SEMUA SOAL BISA PAKE RUMUS CEPAT !!!!
Here we go….
Berikut adalah salah satu Rumus Cepat, Cekidot…

GodBless us...
Senin, 15 April 2013
BELAJAR SISTEM BILANGAN REAL
Sistem bilangan real ini merupakan dasar dari mata kuliah kalkulus 1. Untuk itu matematika universitas memposting materi ini untuk membantu sahabat sharematika dalam belajar kalkulus lanjut1. Sebelum kita memulai materi ini, alangkah baiknya kita berdoa terlebih dahulu.
Berikut materi Kalkulus 1 tentang sistem bilangan real!
Sistem Bilangan Real.
Pada
bagian ini, pembaca diingatkan kembali pada konsep tentang himpunan. Himpunan
adalah sekumpulan obyek/unsur dengan kriteria/syarat tertentu. Unsur-unsur
dalam himpunan S disebut anggota (elemen) S. Himpunan yang tidak
memiliki anggota disebut himpunan kosong, ditulis dengan notasi { }.
Jika
a merupakan anggota himpunan S, maka dibaca “a
elemen S”. Jika a bukan anggota himpunan S, maka dibaca “a bukan elemen S”.
Pada
umumnya, sebarang himpunan dapat dinyatakan dengan 2 cara. Pertama, dengan
mendaftar seluruh anggotanya. Sebagai contoh, himpunan A yang terdiri
atas unsur-unsur 1,2,3,4,5,6,7,8,9 dapat dinyatakan sebagai:
Cara yang kedua,
yaitu dengan menuliskan syarat keanggotaan yang dimiliki oleh seluruh anggota
suatu himpunan tetapi tidak dimiliki oleh unsur-unsur yang bukan anggota
himpunan tersebut. Apabila himpunan A di atas dinyatakan dengan cara
ini, maka dapat ditulis:
Selanjutnya,
akan disampaikan beberapa himpunan bilangan yang dipandang cukup penting.
Bilangan rasional adalah bilangan yang merupakan hasil bagi bilangan bulat dan bilangan asli. Himpunan semua bilangan rasional ditulis dengan notasi Q,
Sedangkan
bilangan phi merupakan hasil bagi
keliling sebarang lingkaran terhadap diameternya (Gambar 1.1.2).
Good Bless
PEMBAHASAN DARI MACAM-MACAM MATRIKS,
Matriks adalah salah satu materi dari mata kuliah aljabar linier dan kali ini kita akan membahas salah satu materi dari aljabar linier ini yang berjudul macam-majam matriks.Sebelum kita mempelajari apa saja macam-macam matriks alangkah baiknya kita mengetahui terlebih dahulu apa itu matriks.
Definisi Matriks.
Matriks adalah susunan elemen-elemen yang berbentuk persegi
panjang atau persegi yang diatur menurut baris-baris dan kolom-kolom
serta ditempatkan dalam tanda kurung biasa atau kurung siku.Setelah kalian tahu definisi matriks mari kita melangkah ke macam-macam matriks :
Pertama.
Matriks persegi atau Matriks bujur sangkar
Matriks persegi adalah matriks yang memiliki baris dan lajur yang sama bentuknya.
m=n.
Contoh matriks persegi :
Kedua.
Matriks Diagonal.
Matriks diagonal adalah matriks yang unsur-unsurnya semua bernilai nol kecuali pada diagonal utamanya.
Contoh Matriks diagonal:
Ketiga.
Matriks Segitiga.
Matriks segitiga adalah matriks yang semua unsur diatas diagonal utamanya bernilai no, ataupun dibawah diagonal utamanya bernilai nol.
Contoh matriks segitiga :
Keempat.
Matriks Setangkup atau matriks simetris
Matriks satangkup adalah matriks persegi yang unsurnya pada baris ke-i dan ke-j sama nilainya dengan unsur pada kolom ke-j dan ke-i.
Contoh matriks setangkup.
Kelima.
Matriks identitas.
Matriks identitas adalah matriks skalar uang nilai unsur-unsur diagonal utamanya sama dengan satu.
Contoh matriks identitas.
Keenam.
Matriks nol.
Matriks nol adalah matriks yang semua unsur-unsurnya bernilai sama dengan nol.
Contoh matriks nol.
Ketujuh.
Matriks Baris.
Matriks baris adalah matriks yang unsur-unsurnya membentuk suatu baris bilangan.
contoh matriks baris.
( 1 3 2 7 5 )
Kedelapan.
Matriks Kolom.
Matriks kolom adalah matriks yang unsur-unsurnya membentuk suatu kolom.
Contoh matriks kolom.
Sumber : http://matematikauniversitas.blogspot.com
BELAJAR ALJABAR LINIER
Aljabar dasar, yang mencatat sifat-sifat operasi bilangan riil,
menggunakan simbol sebagai “pengganti” untuk menandakan konstanta dan
variabel, dan mempelajari aturan tentang ungkapan dan persamaan
matematis yang melibatkan simbol-simbol tersebut.
-
Aljabar abstrak, yang secara aksiomatis mendefinisikan dan menyelidiki
struktur aljabar seperti kelompok matematika, cincin matematika dan
matematika bidang.
- Aljabar linear, yang mempelajari sifat-sifat khusus ruang vektor (termasuk matriks).
- Aljabar universal, yang mempelajari sifat-sifat yang dimiliki semua struktur aljabar.
- Aljabar komputer, yang mengumpulkan manipulasi simbolis benda-benda matematis
Persamaan Linear & Matriks
Persamaan linear dapat dinyatakan sebagai matriks. Misalnya persamaan:
- 3x1 + 4x2 − 2 x3 = 5
- x1 − 5x2 + 2x3 = 7
- 2x1 + x2 − 3x3 = 9
dapat dinyatakan dalam matriks teraugmentasi sebagai berikut
 Penyelesaian persamaan linier dalam bentuk matriks dapat dilakukan melalui beberapa cara, yaitu dengan eliminasi Gauss atau dapat juga dengan cara eliminasi Gauss-Jordan. Namun, suatu sistem persamaan linier dapat diselesaikan dengan eliminasi Gauss untuk mengubah bentuk matriks teraugmentasi ke dalam bentuk eselon-baris tanpa menyederhanakannya. Cara ini disebut dengan substitusi balik.
Sebuah sisitem persamaan linier dapat dikatakan homogen apabila mempunyai bentuk :
Penyelesaian persamaan linier dalam bentuk matriks dapat dilakukan melalui beberapa cara, yaitu dengan eliminasi Gauss atau dapat juga dengan cara eliminasi Gauss-Jordan. Namun, suatu sistem persamaan linier dapat diselesaikan dengan eliminasi Gauss untuk mengubah bentuk matriks teraugmentasi ke dalam bentuk eselon-baris tanpa menyederhanakannya. Cara ini disebut dengan substitusi balik.
Sebuah sisitem persamaan linier dapat dikatakan homogen apabila mempunyai bentuk :
- a11x1 + a12x2 + ... + a1nxn = 0
- a21x1 + a22x2 + ... + a2nxn = 0
- am1x1 + am2x2 + ... + amnxn = 0
Setiap sistem persamaan linier yang homogen bersifat adalah tetap apabila semua sistem mepunyai x1 = 0 , x2 = 0 , ... , xn =
0 sebagai penyelesaian. Penyelesaian ini disebut solusi trivial.
Apabila mempunyai penyelesaian yang lain maka disebut solusi nontrivial.
Penyelesaian Persamaan Linear dengan Matriks
[Bentuk Eselon-baris
Matriks dapat dikatakan Eselon-baris apabila memenuhi persyaratan berikut :
- 1.) Di setiap baris, angka pertama selain 0 harus 1 (leading 1).
- 2.) Jika ada baris yang semua elemennya nol, maka harus dikelompokkan di baris akhir dari matriks.
- 3.) Jika ada baris yang leading 1 maka leading 1 di bawahnya, angka 1-nya harus berada lebih kanan dari leading 1 di atasnya.
- 4.) Jika kolom yang memiliki leading 1 angka selain 1 adalah nol maka matriks tersebut disebut Eselon-baris tereduksi
Contoh: syarat 1: baris pertama disebut dengan leading 1
-

syarat 2: baris ke-3 dan ke-4 memenuhi syarat 2
-

syarat 3: baris pertama dan ke-2 memenuhi syarat 3
-

syarat 4: matriks dibawah ini memenuhi syarat ke 4 dan disebut Eselon-baris tereduksi
-


Operasi Eliminasi Gauss
Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana (ditemukan oleh Carl Friedrich Gauss). Caranya adalah dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang Eselon-baris.
Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan
linear dengan menggunakan matriks. Caranya dengan mengubah persamaan
linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.
Contoh: Diketahui persamaan linear
- x + 2y + z = 6
- x + 3y + 2z = 9
- 2x + y + 2z = 12
Tentukan Nilai x, y dan z
Jawab:
Bentuk persamaan tersebut ke dalam matriks:
-
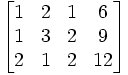
Operasikan Matriks tersebut
 Baris ke 2 dikurangi baris ke 1
Baris ke 2 dikurangi baris ke 1
 Baris ke 3 dikurangi 2 kali baris ke 1
Baris ke 3 dikurangi 2 kali baris ke 1
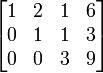 Baris ke 3 ditambah 3 kali baris ke 2
Baris ke 3 ditambah 3 kali baris ke 2
 Baris ke 3 dibagi dengan 3 (Matriks menjadi Eselon-baris)
Maka mendapatkan 3 persamaan linier baru yaitu
Baris ke 3 dibagi dengan 3 (Matriks menjadi Eselon-baris)
Maka mendapatkan 3 persamaan linier baru yaitu
- x + 2y + z = 6
- y + z = 3
- z = 3
Kemudian lakukan substitusi balik maka didapatkan:
- y + z = 3
- y + 3 = 3
- y = 0
- x + 2y + z = 6
- x + 0 + 3 = 6
- x = 3
Jadi nilai dari x = 3 , y = 0 ,dan z = 3

 Baris ke 2 dikurangi baris ke 1
Baris ke 2 dikurangi baris ke 1 Baris ke 3 dikurangi 2 kali baris ke 1
Baris ke 3 dikurangi 2 kali baris ke 1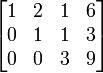 Baris ke 3 ditambah 3 kali baris ke 2
Baris ke 3 ditambah 3 kali baris ke 2 Baris ke 3 dibagi dengan 3 (Matriks menjadi Eselon-baris)
Baris ke 3 dibagi dengan 3 (Matriks menjadi Eselon-baris)Belajar Matriks dan Memahaminya..
Membuat Matriks
Istilah matriks dan array sering digunakan secara bergantian. Lebih tepatnya, adalah matriks adalah array dua dimensi persegi panjang dari bilangan real atau kompleks yang merupakan transformasi linear. Operasi aljabar linear didefinisikan pada matriks telah menemukan aplikasi dalam berbagai bidang teknik. (The Simbolik Math Toolbox opsional memperluas kemampuan MATLAB untuk operasi pada berbagai jenis matriks nonnumeric.
MATLAB memiliki puluhan fungsi yang menciptakan berbagai jenis matriks. Dua dari mereka dapat digunakan untuk membuat sepasang 3-by-3 matriks contoh untuk digunakan di seluruh bab ini. Contoh pertama adalah simetris.
A = pascal(3)
A =
1 1 1
1 2 3
1 3 6
Contoh kedua adalah tidak simetris.
B = magic(3)
B =
8 1 6
3 5 7
4 9 2
Contoh lain adalah matriks 3-by-2 persegi panjang dari bilangan bulat acak.
C = fix(10*rand(3,2))
C =
9 4
2 8
6 7
Sebuah vektor kolom adalah-m-1 matriks, vektor baris adalah 1-by-n matriks dan skalar adalah 1-by-1 matriks. pernyataan
u = [3; 1; 4]
v = [2 0 -1]
s = 7
menghasilkan vektor kolom, vektor baris, dan skalar.
u =
3
1
4
v =
2 0 -1
s =
7
Menambah dan Dengan mengurangi Matriks
Penambahan dan pengurangan matriks didefinisikan seperti itu untuk array, elemen-oleh-elemen. Menambahkan A ke B dan kemudian mengurangkan A dari hasil pulih B.
A = pascal(3);
B = magic(3);
X = A + B
X =
9 2 7
4 7 10
5 12 8
Y = X – A
Y =
8 1 6
3 5 7
4 9 2
Penambahan dan pengurangan matriks memerlukan keduanya memiliki dimensi yang sama, atau salah satunya berupa sebuah. Jika dimensi tidak kompatibel, sebuah hasil kesalahan.
C = fix(10*rand(3,2))
X = A + C
Error using ==> +
Matrix dimensions must agree.
w = v + s
w =
9 7 6
Vektor Produk dan Transpose
Sebuah vektor baris dan vektor kolom panjang yang sama dapat dikalikan dalam rangka baik. Hasilnya adalah baik skalar, produk dalam, atau, matriks produk luar.
u = [3; 1; 4];
v = [2 0 -1];
x = v*u
x =
2
X = u*v
X =
6 0 -3
2 0 -1
8 0 -4
Untuk matriks riil, operasi transposisi dan simpang susun. MATLAB menggunakan tanda kutip (atau kutip tunggal) untuk menunjukkan merefleksikan. contoh kami matriks A adalah simetris, sehingga A “adalah sama dengan A. Tapi B tidak simetris.
B = magic(3);
X = B’
X =
8 3 4
1 5 9
6 7 2
Transposisi ternyata vektor baris ke dalam vektor kolom.
x = v’
x =
2
0
-1
Jika x dan y keduanya vektor kolom nyata, produk x * y tidak didefinisikan, tetapi kedua produk
x’*y
dan
y’*x
adalah skalar yang sama. kuantitas ini digunakan begitu sering, ia memiliki tiga nama yang berbeda: hasil kali dalam, produk skalar, atau dot product.
Untuk vektor kompleks atau matriks, z, kuantitas z ‘menunjukkan transpose konjugasi kompleks, di mana tanda bagian kompleks dari setiap elemen terbalik. The transpose kompleks unconjugated, di mana bagian kompleks setiap elemen mempertahankan tandanya, dilambangkan oleh z. ‘. Jadi jika
z = [1+2i 3+4i]
maka z adalah
1-2i
3-4i
sementara z. ‘ adalah
1+2i
3+4i
Untuk vektor kompleks, kedua produk skalar ‘* y dan y’ x * x adalah kompleks konjugat satu sama lain dan produk skalar * x ‘x dari vektor kompleks dengan itu sendiri adalah nyata.
Mengalikan Matriks
Perkalian matriks didefinisikan dengan cara yang mencerminkan komposisi transformasi linear yang mendasari dan memungkinkan representasi kompak sistem persamaan linier simultan. Produk Matriks C = AB didefinisikan jika ukuran kolom A adalah sama dengan dimensi baris B, atau ketika salah satunya adalah skalar. Jika A adalah m-oleh-p dan B p-by-n, C produk mereka adalah m-by-n. Produk ini sebenarnya dapat didefinisikan dengan menggunakan MATLAB untuk loop, notasi kolon, dan vektor dot produk.
A = pascal(3);
B = magic(3);
m = 3; n = 3;
for i = 1:m
for j = 1:n
C(i,j) = A(i,:)*B(:,j);
end
end
MATLAB menggunakan tanda bintang tunggal untuk menunjukkan perkalian matriks. Dua contoh berikut menggambarkan fakta bahwa perkalian matriks tidak komutatif, AB biasanya tidak sama dengan BA.
X = A*B
X =
15 15 15
26 38 26
41 70 39
Y = B*A
Y =
15 28 47
15 34 60
15 28 43
Sebuah matriks dapat dikalikan di sebelah kanan oleh vektor kolom dan di sebelah kiri dengan vektor baris.
u = [3; 1; 4];
x = A*u
x =
8
17
30
v = [2 0 -1];
y = v*B
y =
12 -7 10
perkalian matriks Rectangular harus memenuhi kondisi dimensi kompatibilitas.
C = memperbaiki (rand * 10 (3,2));
C = fix(10*rand(3,2));
X = A*C
X =
17 19
31 41
51 70
Y = C*A
Error using ==> *
Inner matrix dimensions must agree.
Sesuatu dapat dikalikan dengan skalar.
s = 7;
w = s*v
w =
14 0 -7
Sumber :http://blog.student.uny.ac.id
Langganan:
Postingan (Atom)


















